Svaka osoba tokom svog života susreće se sa telima koja su u jednom od tri agregatna stanja materije. Najjednostavnije agregatno stanje za proučavanje je plin. U članku ćemo razmotriti koncept idealnog plina, dati jednačinu stanja sistema, a također ćemo obratiti pažnju na opis apsolutne temperature.
Stanje plina
Svaki učenik ima dobru predstavu o kojem stanju materije govori kada čuje riječ "gas". Ova riječ se razumije kao tijelo koje je sposobno zauzeti bilo koji volumen koji mu se daje. Nije u stanju da zadrži svoj oblik, jer ne može da odoli ni najmanjem spoljašnjem uticaju. Takođe, gas ne zadržava zapreminu, što ga razlikuje ne samo od čvrstih materija, već i od tečnosti.
Poput tečnosti, gas je fluidna supstanca. U procesu kretanja čvrstih tijela u plinovima, ova potonja ometaju ovo kretanje. Rezultirajuća sila naziva se otpor. Njegova vrijednost zavisi odbrzina tijela u gasu.
Jaki primjeri plinova su zrak, prirodni plin koji se koristi za grijanje domova i kuhanje, inertni plinovi (Ne, Ar) koji se koriste za punjenje reklamnih usijanih cijevi ili se koriste za stvaranje inertnog (neagresivnog, zaštitnog) okruženja pri zavarivanju.
Idealni plin
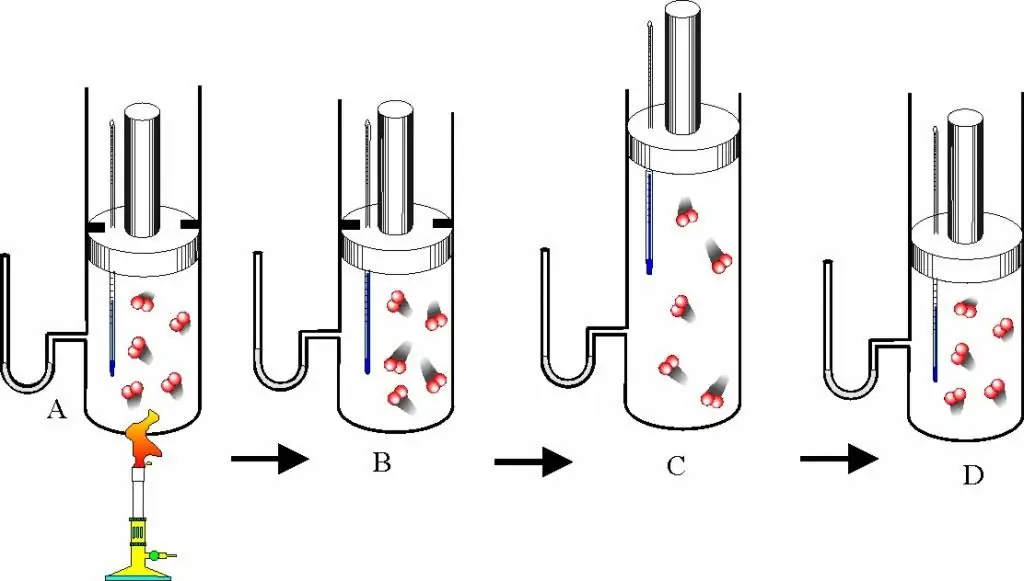
Pre nego što pređete na opis zakona o gasu i jednačine stanja, trebalo bi da dobro razumete pitanje šta je idealan gas. Ovaj koncept je uveden u molekularnu kinetičku teoriju (MKT). Idealan plin je svaki plin koji zadovoljava sljedeće karakteristike:
- Čestice koje ga formiraju ne stupaju u interakciju jedna s drugom osim u slučaju direktnih mehaničkih sudara.
- Kao rezultat sudara čestica sa zidovima posude ili između njih, njihova kinetička energija i impuls su očuvani, odnosno sudar se smatra apsolutno elastičnim.
- Čestice nemaju dimenzije, ali imaju konačnu masu, odnosno slične su materijalnim tačkama.
Prirodno je da bilo koji plin nije idealan, već stvaran. Ipak, za rješavanje mnogih praktičnih problema, ove aproksimacije su prilično valjane i mogu se koristiti. Postoji opće empirijsko pravilo koje kaže: bez obzira na kemijsku prirodu, ako plin ima temperaturu iznad sobne temperature i tlak reda atmosferskog ili nižeg, onda se može smatrati idealnim s velikom preciznošću i može se koristiti za opisivanje to.formula idealne gasne jednadžbe stanja.
Clapeyron-Mendelejev zakon
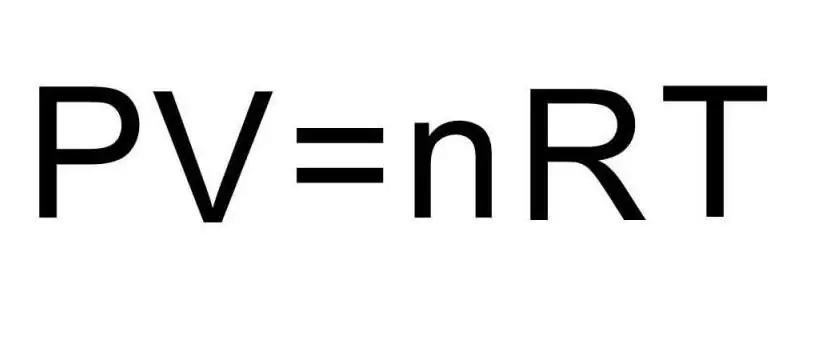
Tranzicijama između različitih agregatnih stanja materije i procesa unutar jednog agregatnog stanja upravlja termodinamika. Pritisak, temperatura i zapremina su tri veličine koje jedinstveno definišu bilo koje stanje termodinamičkog sistema. Formula za jednadžbu stanja idealnog gasa kombinuje sve tri ove veličine u jednu jednakost. Napišimo ovu formulu:
PV=nRT
Ovde P, V, T - pritisak, zapremina, temperatura, respektivno. Vrijednost n je količina tvari u molovima, a simbol R označava univerzalnu konstantu plinova. Ova jednakost pokazuje da što je veći proizvod pritiska i zapremine, veći mora biti proizvod količine supstance i temperature.

Formula za jednadžbu stanja gasa naziva se Clapeyron-Mendelejev zakon. Godine 1834. francuski naučnik Emile Clapeyron, sumirajući eksperimentalne rezultate svojih prethodnika, došao je do ove jednačine. Međutim, Clapeyron je koristio brojne konstante, koje je Mendeljejev kasnije zamijenio jednom - univerzalnom plinskom konstantom R (8, 314 J / (molK)). Stoga je u modernoj fizici ova jednačina dobila ime po imenima francuskih i ruskih naučnika.

Ostali oblici jednadžbi
Iznad smo napisali Mendeljejev-Klapejronovu jednačinu stanja za idealni gas u opšteprihvaćenom ipogodan oblik. Međutim, u problemima u termodinamici često se može zahtijevati nešto drugačiji oblik. Ispod su napisane još tri formule, koje direktno slijede iz napisane jednačine:
PV=NkBT;
PV=m/MRT;
P=ρRT/M.
Ove tri jednačine su univerzalne i za idealan gas, samo što se u njima pojavljuju takve veličine kao što su masa m, molarna masa M, gustina ρ i broj čestica N koje čine sistem. Simbol kB ovdje označava Boltzmannu konstantu (1, 3810-23J/K).
Boyle-Mariotte Law
Kada je Clapeyron sastavio svoju jednačinu, temeljio se na zakonima o plinu koji su eksperimentalno otkriveni nekoliko decenija ranije. Jedan od njih je Boyle-Mariotteov zakon. Odražava izotermni proces u zatvorenom sistemu, zbog čega se mijenjaju makroskopski parametri poput tlaka i volumena. Ako stavimo T i n konstantu u jednadžbu stanja za idealni plin, tada će zakon o plinu imati oblik:
P1V1=P2V 2
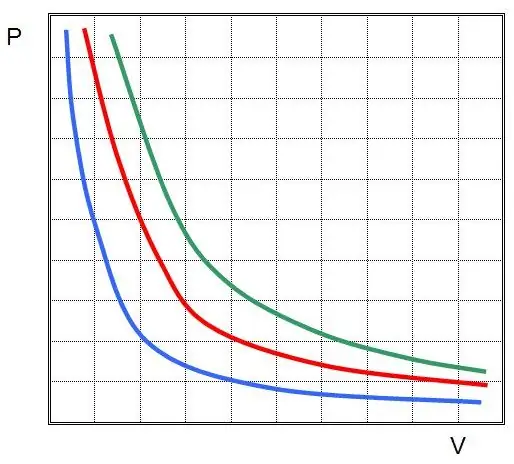
Ovo je Boyle-Mariotteov zakon, koji kaže da se proizvod pritiska i zapremine čuva tokom proizvoljnog izotermnog procesa. U ovom slučaju, same vrijednosti P i V se mijenjaju.
Ako nacrtate P(V) ili V(P), tada će izoterme biti hiperbole.
Zakoni Charlesa i Gay-Lusaca
Ovi zakoni matematički opisuju izobarične i izohorneprocesi, odnosno takvi prelazi između stanja gasnog sistema, u kojima se zadržava pritisak i zapremina. Charlesov zakon se matematički može napisati na sljedeći način:
V/T=const kada je n, P=const.
Gay-Lussacov zakon je napisan na sljedeći način:
P/T=const kada je n, V=const.
Ako su obje jednakosti predstavljene u obliku grafikona, onda ćemo dobiti prave linije koje su nagnute pod nekim uglom prema x-osi. Ovaj tip grafikona pokazuje direktnu proporcionalnost između zapremine i temperature pri konstantnom pritisku i između pritiska i temperature pri konstantnoj zapremini.
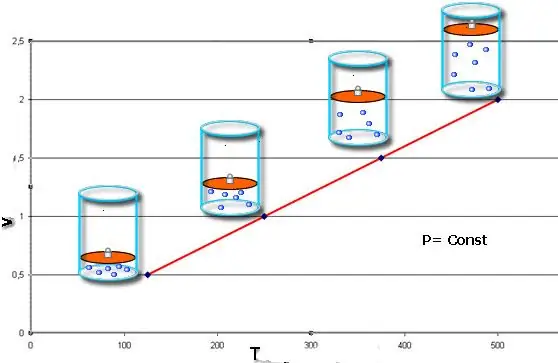
Imajte na umu da sva tri razmatrana zakona o gasu ne uzimaju u obzir hemijski sastav gasa, kao ni promenu njegove količine materije.
Apsolutna temperatura
U svakodnevnom životu navikli smo da koristimo Celzijusovu temperaturnu skalu, jer je zgodna za opisivanje procesa oko nas. Dakle, voda ključa na 100 oC i smrzava se na 0 oC. U fizici se ispostavlja da je ova skala nezgodna, stoga se koristi takozvana apsolutna temperaturna skala, koju je uveo Lord Kelvin sredinom 19. stoljeća. U skladu sa ovom skalom, temperatura se mjeri u Kelvinima (K).
Vjeruje se da na temperaturi od -273,15 oC nema termičkih vibracija atoma i molekula, njihovo kretanje naprijed potpuno prestaje. Ova temperatura u stepenima Celzijusa odgovara apsolutnoj nuli u Kelvinima (0 K). Iz ove definicijefizičko značenje apsolutne temperature slijedi: to je mjera kinetičke energije čestica koje čine materiju, na primjer, atoma ili molekula.
Pored gore navedenog fizičkog značenja apsolutne temperature, postoje i drugi pristupi razumijevanju ove količine. Jedan od njih je spomenuti Charlesov zakon o plinu. Napišimo to u sljedećem obliku:
V1/T1=V2/T 2=>
V1/V2=T1/T 2.
Poslednja jednakost kaže da pri određenoj količini supstance u sistemu (na primer, 1 mol) i određenom pritisku (na primer, 1 Pa), zapremina gasa jedinstveno određuje apsolutnu temperaturu. Drugim riječima, povećanje zapremine gasa u ovim uslovima moguće je samo zbog povećanja temperature, a smanjenje zapremine ukazuje na smanjenje vrednosti T.
Podsjetimo da, za razliku od Celzijusove temperature, apsolutna temperatura ne može biti negativna.
Avogadro princip i mješavine plinova
Pored gore navedenih zakona o gasu, jednačina stanja idealnog gasa takođe vodi do principa koji je otkrio Amedeo Avogadro početkom 19. veka, a koji nosi njegovo prezime. Ovaj princip utvrđuje da je zapremina bilo kog gasa pri konstantnom pritisku i temperaturi određena količinom supstance u sistemu. Odgovarajuća formula izgleda ovako:
n/V=const kada je P, T=const.
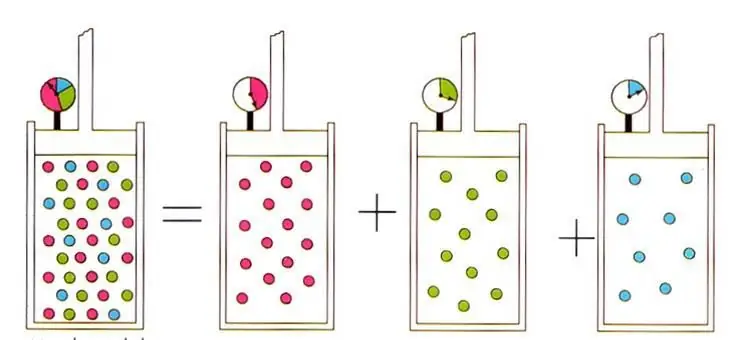
Pisani izraz vodi do dobro poznatog u fizici idealnih gasova D altonovog zakona za gasne mešavine. Ovozakon kaže da je parcijalni pritisak gasa u smeši jedinstveno određen njegovom atomskom frakcijom.
Primjer rješavanja problema
U zatvorenoj posudi sa čvrstim zidovima koja sadrži idealan gas, usled zagrevanja, pritisak se povećao za 3 puta. Potrebno je odrediti konačnu temperaturu sistema ako je njegova početna vrijednost bila 25 oC.
Prvo, pretvorimo temperaturu iz stepeni Celzijusa u Kelvine, imamo:
T=25 + 273, 15=298, 15 K.
Pošto su zidovi posude kruti, proces zagrijavanja se može smatrati izohoričnim. Za ovaj slučaj primjenjujemo Gay-Lussac zakon, imamo:
P1/T1=P2/T 2=>
T2=P2/P1T 1.
Dakle, konačna temperatura se određuje iz proizvoda odnosa pritiska i početne temperature. Zamjenom podataka u jednakost, dobijamo odgovor: T2=894,45 K. Ova temperatura odgovara 621,3 oC.






