U termodinamici, prilikom proučavanja prelaza iz početnog u konačno stanje sistema, važno je poznavati toplotni efekat procesa. Koncept toplotnog kapaciteta je usko povezan sa ovim efektom. U ovom članku ćemo razmotriti pitanje šta se podrazumijeva pod izohornim toplinskim kapacitetom plina.
Idealni plin
Idealni plin je plin čije se čestice smatraju materijalnim tačkama, odnosno nemaju dimenzije, ali imaju masu, i u kojem se sva unutrašnja energija sastoji isključivo od kinetičke energije kretanja molekula i atomi.
Bilo koji pravi gas u idealnom slučaju nikada neće zadovoljiti opisani model, pošto njegove čestice još uvek imaju neke linearne dimenzije i međusobno deluju koristeći slabe van der Waalsove veze ili hemijske veze drugog tipa. Međutim, pri niskim pritiscima i visokim temperaturama, udaljenosti između molekula su velike, a njihova kinetička energija premašuje potencijalnu za desetine puta. Sve ovo omogućava da se sa visokim stepenom tačnosti primeni idealan model za prave gasove.
Unutarnja energija gasa
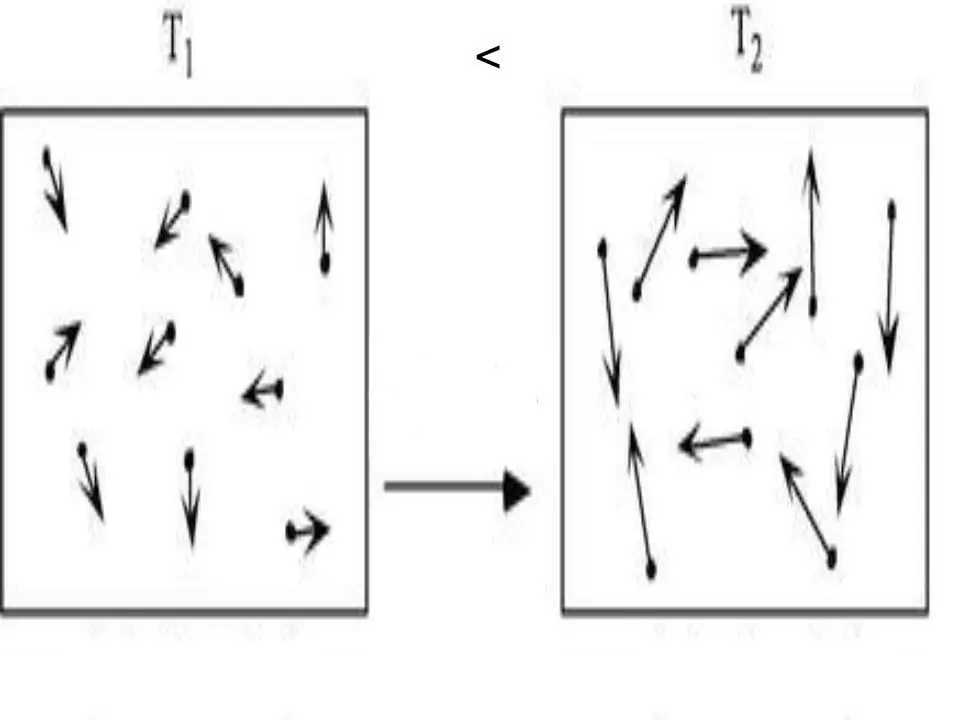
Unutarnja energija bilo kog sistema je fizička karakteristika, koja je jednaka zbiru potencijalne i kinetičke energije. Pošto se potencijalna energija može zanemariti u idealnim gasovima, za njih možemo napisati jednakost:
U=Ek.
Gdje je Ek energija kinetičkog sistema. Koristeći molekularnu kinetičku teoriju i primjenom univerzalne Clapeyron-Mendelejevove jednadžbe stanja, nije teško dobiti izraz za U. Dolje je napisano:
U=z/2nRT.
Ovde su T, R i n apsolutna temperatura, gasna konstanta i količina supstance, respektivno. Z-vrijednost je cijeli broj koji pokazuje broj stupnjeva slobode koje ima molekul plina.
Izobarični i izohorni toplotni kapacitet
U fizici, toplotni kapacitet je količina toplote koja se mora predati sistemu koji se proučava da bi se zagrejao za jedan kelvin. Tačna je i obrnuta definicija, to jest, toplotni kapacitet je količina toplote koju sistem oslobađa kada se ohladi za jedan kelvin.
Najlakši način za sistem je određivanje izohornog toplotnog kapaciteta. Podrazumijeva se kao toplinski kapacitet pri konstantnoj zapremini. Pošto sistem ne obavlja rad u takvim uslovima, sva energija se troši na povećanje unutrašnjih energetskih rezervi. Označimo izohorični toplotni kapacitet simbolom CV, tada možemo napisati:
dU=CVdT.
To jest, promjena unutrašnje energijeSistem je direktno proporcionalan promjeni njegove temperature. Ako uporedimo ovaj izraz sa jednakošću napisanom u prethodnom pasusu, dolazimo do formule za CV u idealnom gasu:
SV=z/2nR.
Ovu vrijednost je nezgodno koristiti u praksi, jer zavisi od količine supstance u sistemu. Stoga je uveden koncept specifičnog izohornog toplotnog kapaciteta, odnosno vrijednosti koja se računa ili na 1 mol plina ili na 1 kg. Označimo prvu vrijednost simbolom CV, drugu - simbolom CV m. Za njih možete napisati sljedeće formule:
CV=z/2R;
CVm=z/2R/M.
Ovdje M je molarna masa.
Izobarični je toplotni kapacitet uz održavanje konstantnog pritiska u sistemu. Primjer takvog procesa je širenje plina u cilindru ispod klipa kada se zagrije. Za razliku od izohornog procesa, tokom izobarnog procesa, toplota koja se dovodi u sistem troši se na povećanje unutrašnje energije i za obavljanje mehaničkog rada, odnosno:
H=dU + PdV.
Entapija izobarnog procesa je proizvod izobarnog toplotnog kapaciteta i promjene temperature u sistemu, odnosno:
H=CPdT.
Ako uzmemo u obzir ekspanziju pri konstantnom pritisku od 1 mol gasa, tada će prvi zakon termodinamike biti zapisan kao:
CPdT=CV dT + RdT.
Posljednji član se dobija iz jednačineClapeyron-Mendeleev. Iz ove jednakosti slijedi odnos između izobarnog i izohornog toplotnog kapaciteta:
CP=CV + R.
Za idealan gas, specifični molarni toplotni kapacitet pri konstantnom pritisku je uvek veći od odgovarajuće izohorične karakteristike za R=8, 314 J/(molK).
Stepeni slobode molekula i toplotni kapacitet
Napišimo ponovo formulu za specifični molarni izohorični toplotni kapacitet:
CV=z/2R.
U slučaju jednoatomskog gasa, vrijednost z=3, pošto se atomi u svemiru mogu kretati samo u tri nezavisna smjera.
Ako govorimo o plinu koji se sastoji od dvoatomskih molekula, na primjer, kiseonik O2 ili vodonik H2, onda, pored translacionog kretanja, ovi molekuli se još uvijek mogu rotirati oko dvije međusobno okomite ose, odnosno z će biti jednako 5.
Za složenije molekule, koristite z=6. da odredite CV






