Titius-Bodeovo pravilo (ponekad jednostavno nazvano Bodeov zakon) je hipoteza da se tijela u nekim orbitalnim sistemima, uključujući Sunce, rotiraju duž poluosi u zavisnosti od planetarnog niza. Formula sugerira da će, šireći se prema van, svaka planeta biti oko dva puta udaljenija od Sunca od prethodne.
Hipoteza je tačno predvidela orbite Cerere (u asteroidnom pojasu) i Urana, ali nije uspela da odredi orbitu Neptuna i na kraju je zamenjena teorijom formiranja Sunčevog sistema. Ime je dobio po Johannu Danielu Titiusu i Johannu Elert Bodeu.

Origins
Prvi spomen serije koja aproksimira Bodeov zakon može se naći u Elementima astronomije Davida Gregoryja, objavljenom 1715. godine. U njemu on kaže: „… pod pretpostavkom da je udaljenost od Sunca do Zemlje podijeljena na deset jednakih dijelova, od kojih će udaljenost Merkura biti oko četiri, od Venere sedam, od Marsa petnaest, od Jupitera pedeset dva, a od Saturna devedeset pet . Sličan prijedlog, vjerovatno inspiriran Gregoryjem, pojavljuje se u djelu koje je objavio Christian Wolff 1724.
Godine 1764, Charles Bonnet je u svojoj knjizi Contemplation of Nature rekao: "Poznajemo sedamnaest planeta koje čine naš Sunčev sistem [to jest, glavne planete i njihove satelite], ali nismo sigurni da njih više nema." Ovome je u svom prijevodu Bonnetovog djela iz 1766. Johann Daniel Titius dodao dva svoja pasusa na dnu stranice 7 i na vrhu stranice 8. Novi interpolirani pasus se ne nalazi u Bonnetovom originalnom tekstu: niti u italijanskom niti engleski prijevodi djela.
Otkriće Ticija
Postoje dva dijela u interkaliranom Titijevom tekstu. Prvi objašnjava slijed planetarnih udaljenosti od Sunca. Sadrži i nekoliko riječi o udaljenosti od Sunca do Jupitera. Ali ovo nije kraj teksta.
Vrijedi reći nekoliko riječi o formuli Titius-Bodeovog pravila. Obratite pažnju na udaljenosti između planeta i otkrijte da su gotovo sve odvojene jedna od druge u omjeru koji odgovara njihovim tjelesnim veličinama. Podijelite udaljenost od Sunca do Saturna sa 100 dijelova; tada je Merkur odvojen sa četiri takva dela od Sunca; Venera - na 4 + 3=7 takvih dijelova; Zemlja - za 4+6=10; Mars - od 4+12=16.
Ali imajte na umu da od Marsa do Jupitera postoji odstupanje od ovog tako preciznog napredovanja. Od Marsa slijedi prostor od 4+24=28 takvih dijelova, ali do sada na njemu nije otkrivena niti jedna planeta. Ali da li lord arhitekta treba da ostavi ovo mesto prazno? Nikad. Daklepretpostavimo da ovaj prostor bez sumnje pripada još neotkrivenim mjesecima Marsa, i dodajmo da možda Jupiter još uvijek ima nekoliko manjih mjeseci oko sebe koje još nije vidio nijedan teleskop.

Rise of the Bode
Godine 1772. Johann Elert Bode, u dobi od dvadeset pet godina, završio je drugo izdanje svog astronomskog kompendijuma Anleitung zur Kenntniss des gestirnten Himmels ("Vodič za poznavanje zvjezdanog neba"), u koji je dodao je sljedeću fusnotu, izvorno bez izvora, ali zabilježeno u kasnijim verzijama. U Bodeovim memoarima može se pronaći referenca na Titiusa sa jasnim priznanjem njegovog autoriteta.

Opinion Bode
Ovako zvuči Titius-Bodeovo pravilo u predstavljanju potonjeg: ako se udaljenost od Sunca do Saturna uzme jednakom 100, tada je Merkur odvojen od Sunca za četiri takva dijela. Venera - 4+3=7. Zemlja - 4+6=10. Mars - 4+12=16.
Sada postoji praznina u ovom uređenom napredovanju. Nakon Marsa slijedi prostor sa proračunom 4+24=28, u kojem još nije viđena ni jedna planeta. Možemo li vjerovati da je Osnivač svemira ovaj prostor ostavio praznim? Naravno da ne. Odavde dolazimo do udaljenosti Jupitera u obliku proračuna 4+48=52 i, konačno, do udaljenosti Saturna - 4+96=100.

Ove dvije tvrdnje koje se odnose na svu specifičnu tipologiju i orbitalne radijuse izgleda dolaze iz drevnih vremenaastronomija. Mnoge od ovih teorija datiraju iz vremena prije sedamnaestog stoljeća.
Uticaj
Titius je bio učenik njemačkog filozofa Christiana Freiherra von Wolffa (1679-1754). Drugi dio umetnutog teksta u Bonnetovom djelu baziran je na von Wolffovom djelu iz 1723. godine, Vernünftige Gedanken von den Wirkungen der Natur.
Književnost dvadesetog veka pripisuje autorstvo Titius-Bodeovog pravila jednom nemačkom filozofu. Ako je tako, Titius bi mogao naučiti od njega. Još jednu stariju referencu napisao je James Gregory 1702. u svojoj Astronomiae Physicae et geometryae Elementa, gdje je niz planetarnih udaljenosti 4, 7, 10, 16, 52 i 100 postao geometrijska progresija omjera 2.
Ovo je Newtonova najbliža formula, a pronađena je i u spisima Benjamina Martina i Thomasa Cearda godinama prije nego što je Bonnetova knjiga objavljena u Njemačkoj.
Dalji rad i praktične implikacije
Titius i Bode su se nadali da će zakon dovesti do otkrića novih planeta, i zaista, otkriće Urana i Cerere, između kojih se udaljenost dobro slaže sa zakonom, doprinijelo je njegovom prihvatanju od strane naučnog svijeta.
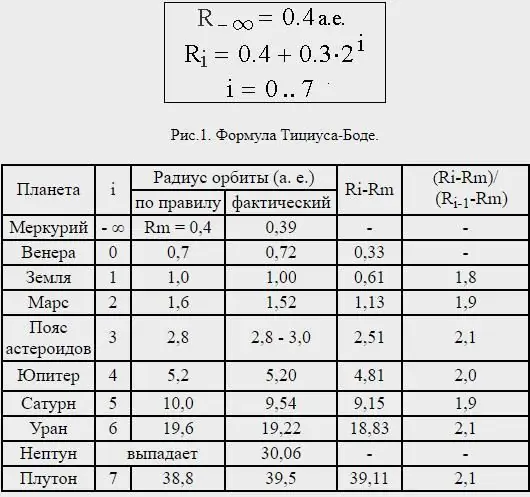
Međutim, Neptunova udaljenost je bila vrlo nedosljedna, a zapravo je Pluton - koji se sada ne smatra planetom - na prosječnoj udaljenosti koja otprilike odgovara Titius-Bodeovom zakonu predviđenom za sljedeću planetu izvan Urana.
Prvobitno objavljeni zakon približno su zadovoljile sve poznate planete - Merkur i Saturn - sa jazom izmeđučetvrta i peta planeta. Ovo se smatralo zanimljivom, ali ne od velike važnosti, sve do otkrića Urana 1781. godine, što se uklapa u seriju.
Na osnovu ovog otkrića, Bode je pozvao na potragu za petom planetom. Ceres, najveći objekat u asteroidnom pojasu, pronađen je na Bodeovom predviđenom položaju 1801. Bodeov zakon je bio široko prihvaćen sve dok Neptun nije otkriven 1846. i pokazano je da nije u skladu sa zakonom.
U isto vrijeme, veliki broj asteroida otkrivenih u pojasu precrtao je Ceres sa liste planeta. O Bodeovom zakonu raspravljao je astronom i logičar Charles Sanders Peirce 1898. godine kao primjer pogrešnog zaključivanja.

Razvoj problema
Otkriće Plutona 1930. dodatno je zakomplikovalo problem. Iako nije odgovarao položaju predviđenom Bodeovim zakonom, radilo se o položaju koji je zakon predviđao za Neptun. Međutim, naknadno otkriće Kuiperovog pojasa, a posebno objekta Eris, koji je masivniji od Plutona, ali nije u skladu s Bodeovim zakonom, dodatno je diskreditirao formulu.
Serdin doprinos
Jezuita Tomas Cerda održao je čuveni kurs astronomije u Barseloni 1760. godine na Kraljevskoj katedri za matematiku na koledžu Sant Jaume de Cordelle (Carsko i Kraljevsko sjemenište plemića iz Cordela). U Cerdasovom Tratadu pojavljuju se planetarne udaljenosti, dobijene primjenom Keplerovog trećeg zakona, s tačnošću od 10-3.
Ako uzmemo za 10 udaljenost od Zemlje izaokružiti na cijeli broj, može se izraziti geometrijska progresija [(Dn x 10) - 4] / [(Dn-1 x 10) - 4]=2, od n=2 do n=8. A koristeći kružno uniformno fiktivno kretanje do Keplerove anomalije, vrijednosti Rn koje odgovaraju omjerima svake planete mogu se dobiti kao rn=(Rn - R1) / (Rn-1 - R1), što rezultira 1,82; 1, 84; 1, 86; 1,88 i 1,90, gdje je rn=2 - 0,02 (12 - n) eksplicitna relacija između Keplerovog kontinuiteta i Titius-Bodeovog zakona, koji se smatra slučajnom numeričkom koincidencijom. Rezultat izračuna je blizu dva, ali se dvojka može smatrati zaokruživanjem broja 1, 82.

Prosječna brzina planete od n=1 do n=8 smanjuje udaljenost od Sunca i razlikuje se od ravnomjernog opadanja na n=2 kako bi se oporavila od n=7 (orbitalna rezonancija). Ovo utiče na udaljenost od Sunca do Jupitera. Međutim, udaljenost između svih ostalih objekata u okviru ozloglašenog pravila kojem je članak posvećen također je određena ovom matematičkom dinamikom.
Teoretski aspekt
Ne postoji čvrsto teorijsko objašnjenje u osnovi Titius-Bodeovog pravila, ali je moguće da imajući u vidu kombinaciju orbitalne rezonancije i nedostatka stepena slobode, bilo koji stabilan planetarni sistem ima veliku vjerovatnoću ponavljanja modela opisanog u ova teorija dvojice naučnika.
Pošto je ovo možda matematička slučajnost, a ne "zakon prirode", ponekad se naziva pravilom, a ne "zakonom". Međutim, astrofizičar Alan Boss tvrdi da je to jednostavnoslučajnost, a planetarni naučni časopis Icarus više ne prihvata članke koji pokušavaju da pruže poboljšane verzije "zakona".
Orbitalna rezonancija
Orbitalna rezonanca velikih orbitirajućih tijela stvara regije oko Sunca koje nemaju dugoročne stabilne orbite. Rezultati simulacije formiranja planeta podržavaju ideju da će nasumično odabran stabilan planetarni sistem vjerovatno zadovoljiti Titius-Bodeovo pravilo.

Dubrulle i Graner
Dubrulle i Graner su pokazali da pravila udaljenosti po stepenu mogu biti posljedica modela kolapsirajućih oblaka planetarnih sistema koji imaju dvije simetrije: rotacionu invarijantnost (olak i njegov sadržaj su osi simetrični) i invarijantnost skale (olak i njegov sadržaj izgleda isto na svim skalama).
Potonje je karakteristika mnogih fenomena za koje se smatra da igraju ulogu u formiranju planeta, kao što je turbulencija. Udaljenost od Sunca do planeta Sunčevog sistema, koju su predložili Titius i Bode, nije revidirana u okviru studija Dubrullea i Granera.






