Postoje objekti koji su u stanju da promene gustinu toka elektromagnetnog zračenja koji pada na njih, odnosno da ga ili povećaju prikupljanjem u jednoj tački, ili smanje raspršivanjem. Ovi objekti se u fizici nazivaju sočivima. Pogledajmo izbliza ovo pitanje.
Šta su sočiva u fizici?
Ovaj koncept označava apsolutno svaki objekat koji je sposoban promijeniti smjer širenja elektromagnetnog zračenja. Ovo je opća definicija sočiva u fizici, koja uključuje optička naočala, magnetna i gravitacijska sočiva.
U ovom članku fokus će biti na optičkim staklima, koje su objekti napravljeni od prozirnog materijala i ograničeni s dvije površine. Jedna od ovih površina mora nužno imati zakrivljenost (tj. biti dio sfere konačnog polumjera), inače objekt neće imati svojstvo promjene smjera širenja svjetlosnih zraka.
Princip sočiva

Suština rada je ovo nekompliciranaoptički objekat je fenomen prelamanja sunčevih zraka. Početkom 17. vijeka, poznati holandski fizičar i astronom Willebrord Snell van Rooyen objavio je zakon refrakcije, koji trenutno nosi njegovo prezime. Formulacija ovog zakona je sljedeća: kada sunčeva svjetlost prođe kroz međuprostor između dva optički prozirna medija, tada je proizvod sinusa upadnog ugla između zraka i normale na površinu i indeksa prelamanja medija u kojem ona se širi je konstantna vrijednost.

Da pojasnimo gore navedeno, dajemo primjer: neka svjetlost padne na površinu vode, dok je ugao između normale na površinu i zraka θ1. Zatim se svjetlosni snop lomi i počinje svoje širenje u vodi već pod uglom θ2 u odnosu na normalu na površinu. Prema Snellovom zakonu, dobijamo: sin(θ1)n1=sin(θ2) n2, gdje su n1 i n2 indeksi loma zraka i vode, odnosno. Šta je indeks loma? Ovo je vrijednost koja pokazuje koliko je puta brzina prostiranja elektromagnetnih valova u vakuumu veća od one za optički prozirni medij, odnosno n=c/v, gdje su c i v brzine svjetlosti u vakuumu i srednji, respektivno.
Fizika pojave prelamanja leži u implementaciji Fermatovog principa, prema kojem se svjetlost kreće tako da u najkraćem vremenu savlada udaljenost od jedne tačke do druge u prostoru.
Vrste sočiva

Tip optičkog sočiva u fizici je određen isključivo oblikom površina koje ga formiraju. Smjer prelamanja zraka koji pada na njih ovisi o ovom obliku. Dakle, ako je zakrivljenost površine pozitivna (konveksna), tada će se, po izlasku iz sočiva, svjetlosni snop širiti bliže svojoj optičkoj osi (vidi dolje). Suprotno tome, ako je zakrivljenost površine negativna (konkavna), tada će se snop, prolazeći kroz optičko staklo, udaljiti od svoje centralne ose.
Opet imajte na umu da površina bilo koje zakrivljenosti lomi zrake na isti način (prema Stelinom zakonu), ali normale na njih imaju drugačiji nagib u odnosu na optičku os, što rezultira različitim ponašanjem prelomljenog zraka.
Sočivo ograničeno s dvije konveksne površine naziva se konvergentno sočivo. Zauzvrat, ako ga formiraju dvije površine s negativnom zakrivljenošću, onda se to naziva raspršenjem. Sve druge vrste optičkih stakala povezuju se sa kombinacijom ovih površina, kojima se dodaje i ravan. Kakvo će svojstvo kombinovano sočivo imati (divergentno ili konvergentno) zavisi od ukupne zakrivljenosti poluprečnika njegovih površina.
Elementi sočiva i svojstva zraka

Da biste ugradili sočiva u fiziku slike, morate se upoznati sa elementima ovog objekta. Oni su navedeni ispod:
- Glavna optička os i centar. U prvom slučaju, oni označavaju pravu liniju koja prolazi okomito na sočivo kroz njegov optički centar. Potonji je, zauzvrat, tačka unutar sočiva, prolazeći kroz koju snop ne doživljava prelamanje.
- Žižna daljina i fokus - rastojanje između centra i tačke na optičkoj osi, koja prikuplja sve zrake koje upadaju na sočivo paralelno sa ovom osom. Ova definicija vrijedi za skupljanje optičkih stakala. U slučaju divergentnih sočiva, same zrake neće konvergirati u tačku, već njihov imaginarni nastavak. Ova tačka se naziva glavni fokus.
- Optička snaga. Ovo je naziv recipročne žižne daljine, odnosno D \u003d 1 / f. Mjeri se u dioptrijama (dioptrijama), odnosno 1 dioptrija.=1 m-1.
Sljedeće su glavne karakteristike zraka koje prolaze kroz sočivo:
- zraka koja prolazi kroz optički centar ne mijenja svoj smjer kretanja;
- zrake koje upadaju paralelno glavnoj optičkoj osi mijenjaju svoj smjer tako da prolaze kroz glavni fokus;
- zrake koje padaju na optičko staklo pod bilo kojim uglom, ali prolaze kroz njegovo fokus, mijenjaju svoj smjer širenja na takav način da postanu paralelne s glavnom optičkom osom.
Navedena svojstva zraka za tanka sočiva u fizici (kako se zovu jer bez obzira kakve sfere su formirane i koliko su debele, samo optička svojstva materije predmeta) koriste se za građenje slika u njima.
Slike u optičkim naočalama: kako napraviti?
Ispod je slika koja detaljno opisuje šeme za konstruisanje slika u konveksnim i konkavnim sočivima objekta(crvena strelica) u zavisnosti od njegovog položaja.
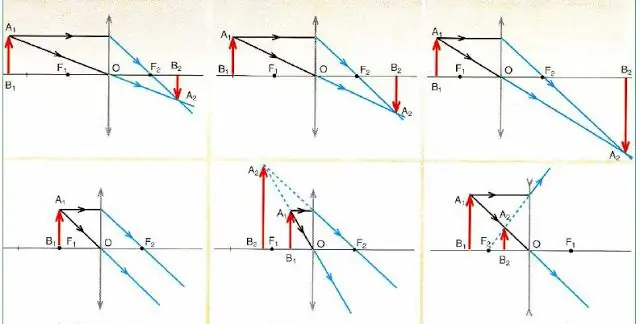
Važni zaključci slijede iz analize kola na slici:
- Bilo koja slika je izgrađena na samo 2 zraka (koji prolaze kroz centar i paralelno sa glavnom optičkom osom).
- Konvergentna sočiva (označena sa strelicama na krajevima okrenutim prema van) mogu dati i uvećanu i smanjenu sliku, koja zauzvrat može biti stvarna (stvarna) ili imaginarna.
- Ako je predmet u fokusu, tada sočivo ne formira njegovu sliku (pogledajte donji dijagram lijevo na slici).
- Rasipajuće optičke naočare (označene strelicama na njihovim krajevima usmjerenim prema unutra) uvijek daju smanjenu i virtuelnu sliku bez obzira na položaj objekta.
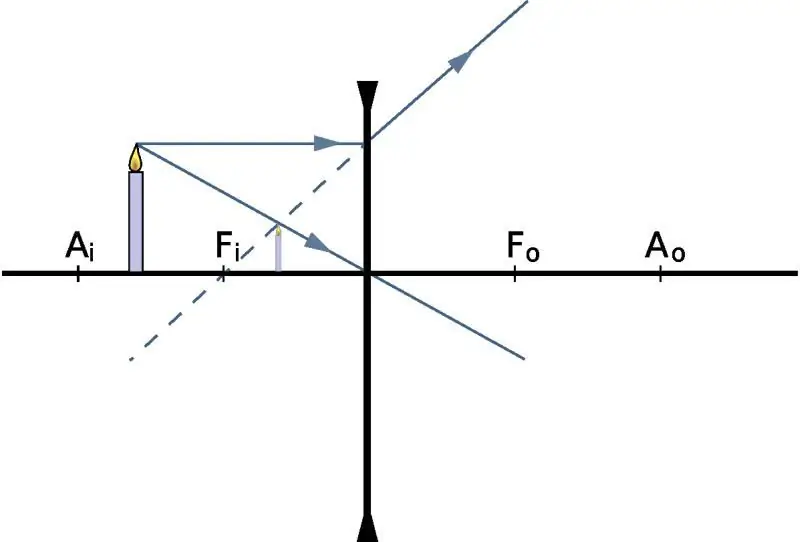
Pronalaženje udaljenosti do slike
Da bismo odredili na kojoj udaljenosti će se slika pojaviti, znajući položaj samog objekta, dajemo formulu sočiva u fizici: 1/f=1/do + 1 /d i, gdje su do i di udaljenost do objekta i njegove slike od optičkog centar, odnosno f je glavni fokus. Ako govorimo o sabirnom optičkom staklu, onda će f-broj biti pozitivan. Obrnuto, za divergentno sočivo, f je negativan.
Upotrijebimo ovu formulu i riješimo jednostavan problem: neka se objekt nalazi na udaljenosti do=2f od centra sabirnog optičkog stakla. Gdje će se pojaviti njegova slika?
Iz uslova zadatka imamo: 1/f=1/(2f)+1/di. Od: 1/di=1/f - 1/(2f)=1/(2f), tj. di=2 f. Dakle, slika će se pojaviti na udaljenosti od dva fokusa od sočiva, ali na drugoj strani od samog objekta (to je naznačeno pozitivnim predznakom vrijednosti di).
Kratka istorija
Zanimljivo je dati etimologiju riječi "objektiv". Potiče od latinskih riječi lens i lentis, što znači "leća", budući da optički objekti svojim oblikom zaista izgledaju kao plod ove biljke.
Snaga prelamanja sfernih prozirnih tijela bila je poznata starim Rimljanima. U tu svrhu koristili su okrugle staklene posude napunjene vodom. Sama staklena sočiva su počela da se izrađuju tek u 13. veku u Evropi. Korišćene su kao alat za čitanje (moderne naočare ili lupa).
Aktivna upotreba optičkih objekata u proizvodnji teleskopa i mikroskopa datira još od 17. veka (početkom ovog veka Galileo je izumeo prvi teleskop). Imajte na umu da je matematičku formulaciju Stelinog zakona refrakcije, bez znanja o kojoj je nemoguće proizvesti sočiva sa željenim svojstvima, objavio holandski naučnik početkom istog 17. veka.
Ostala sočiva
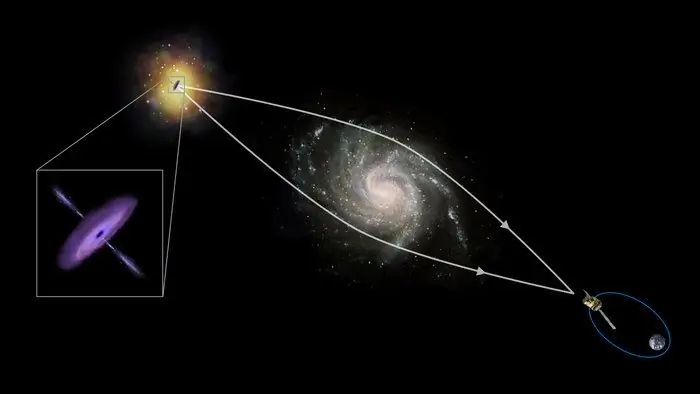
Kao što je gore navedeno, pored optičkih lomnih objekata, postoje i magnetni i gravitacijski objekti. Primjer prvog su magnetna sočiva u elektronskom mikroskopu, živopisan primjer drugog je izobličenje smjera svjetlosnog toka,kada prođe blizu masivnih svemirskih tijela (zvijezde, planete).






