Važan dio termodinamike je proučavanje transformacija između različitih faza supstance, budući da se ovi procesi dešavaju u praksi i od fundamentalnog su značaja za predviđanje ponašanja sistema pod određenim uslovima. Ove transformacije se nazivaju fazni prijelazi, kojima je članak posvećen.
Koncept faze i sistemske komponente

Pre nego što pređemo na razmatranje faznih prelaza u fizici, potrebno je definisati pojam same faze. Kao što je poznato iz kursa opšte fizike, postoje tri agregatna stanja: gasovito, čvrsto i tečno. U posebnom dijelu nauke - u termodinamici - zakoni su formulisani za faze materije, a ne za njihova agregirana stanja. Faza se shvata kao određena zapremina materije koja ima homogenu strukturu, karakteriše se specifičnim fizičkim i hemijskim svojstvima i odvojena je od ostatka materije granicama, koje se nazivaju interfaza.
Dakle, koncept "faze" nosi mnogo praktičnije značajnije informacije o svojstvimamaterija nego njeno agregatno stanje. Na primjer, čvrsto stanje metala kao što je gvožđe može biti u sljedećim fazama: niskotemperaturna magnetna kubika u središtu tijela (BCC), niskotemperaturna nemagnetna bcc, kubika s centriranjem lica (fcc) i visoko- temperatura nemagnetna bcc.
Pored koncepta "faze", zakoni termodinamike koriste i izraz "komponente", koji označava broj hemijskih elemenata koji čine određeni sistem. To znači da faza može biti jednokomponentna (1 hemijski element) ili višekomponentna (nekoliko hemijskih elemenata).
Gibbsova teorema i ravnoteža između faza sistema

Da bi se razumjeli fazni prijelazi, potrebno je poznavati ravnotežne uslove između njih. Ovi uslovi se mogu matematički dobiti rješavanjem sistema Gibbsovih jednačina za svaku od njih, uz pretpostavku da je ravnotežno stanje postignuto kada ukupna Gibbsova energija sistema izolovanog od vanjskih utjecaja prestane da se mijenja.
Kao rezultat rješavanja naznačenog sistema jednadžbi, dobijaju se uslovi za postojanje ravnoteže između nekoliko faza: izolovani sistem će prestati da se razvija tek kada se povećaju pritisci, hemijski potencijali svake komponente i temperature u svim fazama su jednake jedna drugoj.
Gibbsovo fazno pravilo za ravnotežu

Sistem koji se sastoji od nekoliko faza i komponenti može biti u ravnoteži ne samopod određenim uslovima, na primer, pri određenoj temperaturi i pritisku. Neke od varijabli u Gibbsovom teoremu za ravnotežu mogu se mijenjati uz održavanje i broja faza i broja komponenti koje su u ovoj ravnoteži. Broj varijabli koje se mogu promijeniti bez narušavanja ravnoteže u sistemu naziva se broj sloboda ovog sistema.
Broj sloboda l sistema koji se sastoji od f faza i k komponenti je jedinstveno određen Gibbsovim faznim pravilom. Ovo pravilo je matematički zapisano na sljedeći način: l + f=k + 2. Kako raditi s ovim pravilom? Veoma jednostavno. Na primjer, poznato je da se sistem sastoji od f=3 ravnotežne faze. Koliki je minimalni broj komponenti koji takav sistem može sadržavati? Na pitanje možete odgovoriti razmišljanjem na sljedeći način: u slučaju ravnoteže, najstroži uvjeti postoje kada se ona realizuje samo na određenim pokazateljima, odnosno promjena bilo kojeg termodinamičkog parametra će dovesti do neravnoteže. To znači da je broj sloboda l=0. Zamjenom poznatih vrijednosti l i f dobijamo k=1, odnosno sistem u kojem su tri faze u ravnoteži može se sastojati od jedne komponente. Najbolji primjer je trostruka tačka vode, gdje led, tečna voda i para postoje u ravnoteži na određenim temperaturama i pritiscima.
Klasifikacija faznih transformacija
Ako počnete mijenjati neke termodinamičke parametre u sistemu u ravnoteži, možete promatrati kako će jedna faza nestati, a druga će se pojaviti. Jednostavan primjer ovog procesa je otapanje leda kada se zagrije.
S obzirom da Gibbsova jednadžba zavisi samo od dvije varijable (pritisak i temperatura), a fazni prijelaz uključuje promjenu ovih varijabli, onda se matematički prelaz između faza može opisati razlikovanjem Gibbsove energije u odnosu na njenu varijable. Upravo je ovaj pristup koristio austrijski fizičar Paul Ehrenfest 1933. godine, kada je sastavio klasifikaciju svih poznatih termodinamičkih procesa koji se javljaju sa promjenom fazne ravnoteže.
Iz osnova termodinamike slijedi da je prvi izvod Gibbsove energije u odnosu na temperaturu jednak promjeni entropije sistema. Derivat Gibbsove energije u odnosu na pritisak jednak je promjeni zapremine. Ako, kada se faze u sistemu promene, entropija ili zapremina dožive prekid, odnosno naglo se promene, onda govore o faznom prelazu prvog reda.
Dalje, drugi derivati Gibbsove energije u odnosu na temperaturu i pritisak su toplotni kapacitet i koeficijent zapreminskog širenja, respektivno. Ako je transformacija između faza praćena diskontinuitetom u vrijednostima naznačenih fizičkih veličina, onda se govori o faznom prijelazu drugog reda.
Primjeri transformacija između faza

Postoji ogroman broj različitih prijelaza u prirodi. U okviru ove klasifikacije, upečatljivi primeri prelaza prve vrste su procesi topljenja metala ili kondenzacije vodene pare iz vazduha, kada dođe do skoka zapremine u sistemu.
Ako govorimo o prijelazima drugog reda, onda su upečatljivi primjeri transformacija željeza iz magnetnog u paramagnetno stanje na temperaturi768 ºC ili transformacija metalnog provodnika u supravodljivo stanje na temperaturama blizu apsolutne nule.
Jednačine koje opisuju prijelaze prve vrste
U praksi je često potrebno znati kako se temperatura, pritisak i apsorbovana (oslobođena) energija menjaju u sistemu kada se u njemu dešavaju fazne transformacije. U tu svrhu koriste se dvije važne jednačine. Dobijaju se na osnovu poznavanja osnova termodinamike:
- Clapeyronova formula, koja uspostavlja odnos između pritiska i temperature tokom transformacija između različitih faza.
- Clausiusova formula koja povezuje apsorbovanu (oslobođenu) energiju i temperaturu sistema tokom transformacije.
Upotreba obe jednadžbe nije samo u dobijanju kvantitativnih zavisnosti fizičkih veličina, već i u određivanju predznaka nagiba ravnotežnih krivulja na faznim dijagramima.
Jednačina za opisivanje prijelaza druge vrste

Fazni prijelazi 1. i 2. vrste opisani su različitim jednačinama, pošto primjena Clausiusovih i Clausiusovih jednačina za prelaze drugog reda dovodi do matematičke nesigurnosti.
Da bi se opisali potonje, koriste se Ehrenfestove jednadžbe, koje uspostavljaju odnos između promjena tlaka i temperature kroz poznavanje promjena toplotnog kapaciteta i koeficijenta zapreminskog širenja tokom procesa transformacije. Ehrenfestove jednadžbe se koriste za opisivanje prijelaza provodnik-supervodič u odsustvu magnetnog polja.
Važnostfazni dijagrami
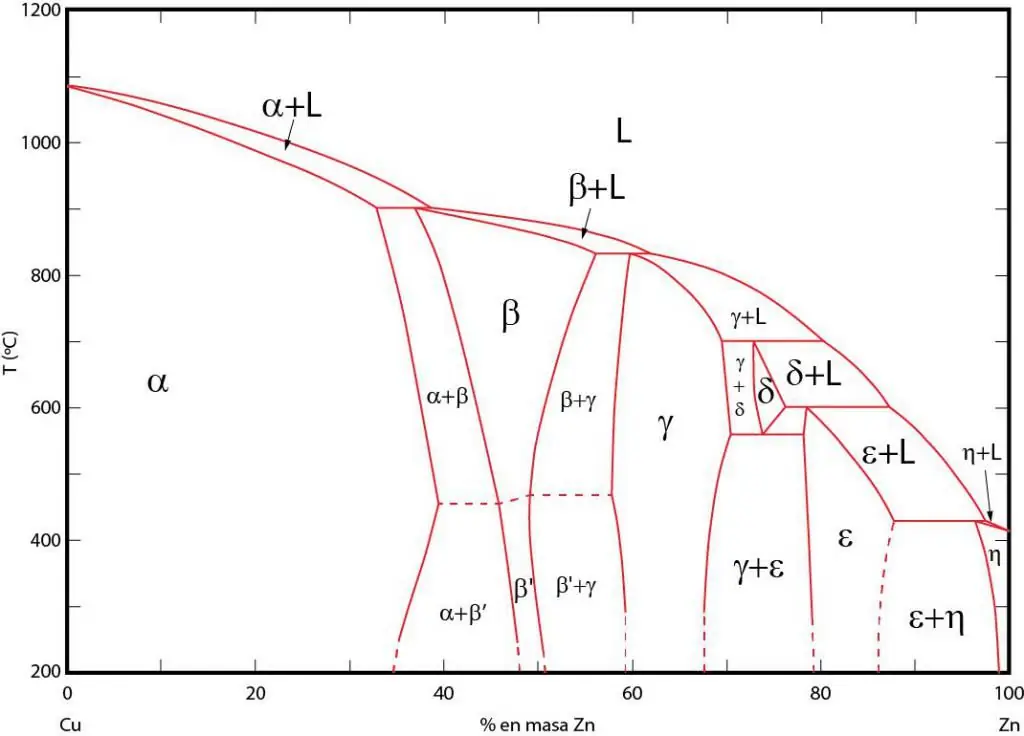
Fazni dijagrami su grafički prikaz područja u kojima odgovarajuće faze postoje u ravnoteži. Ove oblasti su odvojene ravnotežnim linijama između faza. Često se koriste fazni dijagrami P-T (pritisak-temperatura), T-V (temperatura-zapremina) i P-V (pritisak-zapremina).
Važnost faznih dijagrama leži u činjenici da vam omogućavaju da predvidite u kojoj će fazi biti sistem kada se vanjski uslovi u skladu s tim promijene. Ova informacija se koristi u termičkoj obradi različitih materijala kako bi se dobila struktura sa željenim svojstvima.






