Rad sila trenja mirovanja, klizanja i kotrljanja. Formule i primjeri problema

2024 Autor: Angel Austin | [email protected]. Zadnja izmjena: 2024-01-02 17:42

U posebnom dijelu fizike - dinamici, kada proučavaju kretanje tijela, razmatraju sile koje djeluju na pokretni sistem. Potonji mogu obavljati i pozitivan i negativan rad. Razmotrite u ovom članku šta je rad sile trenja i kako se on izračunava.

Koncept rada u fizici

U fizici se koncept "rad" razlikuje od uobičajene ideje ove riječi. Rad se podrazumijeva kao fizička veličina, koja je jednaka skalarnom proizvodu vektora sile i vektora pomaka tijela. Pretpostavimo da postoji neki objekat na koji deluje sila F¯. Kako na njega ne djeluju druge sile, vektor njegovog pomaka l¯ će se poklopiti u smjeru s vektorom F¯. Skalarni proizvod ovih vektora u ovom slučaju će odgovarati proizvodu njihovih modula, odnosno:

A=(F¯l¯)=Fl.

Vrijednost A je rad koji izvrši sila F¯ da pomjeri objekt za udaljenost l. Uzimajući u obzir dimenzije vrijednosti F i l, nalazimo da se rad mjeri u njutnima po metru (Nm) u SI sistemu. Međutim, jedinicaNm ima svoje ime - to je džul. To znači da je koncept rada isti kao i koncept energije. Drugim riječima, ako sila od 1 njutna pomjeri tijelo za 1 metar, tada su odgovarajući troškovi energije 1 džul.

Kolika je sila trenja?

Proučavanje pitanja rada sile trenja moguće je ako znate o kojoj vrsti sile je riječ. Trenje u fizici je proces koji sprečava bilo kakvo kretanje jednog tijela na površini drugog kada se ove površine dovedu u kontakt.

Ako uzmemo u obzir samo čvrsta tijela, onda za njih postoje tri vrste trenja:

• odmor;
• slip;
• rolling.

Ove sile djeluju između dodirnih površina i uvijek su usmjerene protiv kretanja tijela.

Trenje mirovanja sprečava samo kretanje, trenje klizanja se manifestuje u procesu kretanja, kada površine tela klize jedna preko druge, a trenje kotrljanja postoji između tela koje se kotrlja po površini i same površine.

Primjer djelovanja statičkog trenja je automobil koji je na ručnoj kočnici na padini. Trenje klizanja se manifestira kada se skijaš kreće po snijegu ili klizač po ledu. Konačno, trenje kotrljanja djeluje dok se točak automobila kreće po cesti.

Sile za sve tri vrste trenja se izračunavaju pomoću sljedeće formule:

F_t=µ_tN.

Ovdje je N sila reakcije oslonca, µ_t je koeficijent trenja. Sila Npokazuje veličinu udarca oslonca na tijelo okomito na ravan površine. Što se tiče parametra µ_{t, on se eksperimentalno mjeri za svaki par materijala za trljanje, na primjer, drvo-drvo, čelik-snijeg, itd. Izmjereni rezultati se prikupljaju u posebne tabele.}

Za svaku silu trenja, koeficijent µ_{t ima svoju vrijednost za odabrani par materijala. Dakle, koeficijent statičkog trenja veći je od koeficijenta trenja klizanja za nekoliko desetina posto. Zauzvrat, koeficijent kotrljanja je 1-2 reda veličine manji od onog za klizanje.}

Rad sila trenja

Sada, nakon što ste se upoznali s konceptima rada i vrstama trenja, možete prijeći direktno na temu članka. Razmotrimo redom sve vrste sila trenja i shvatimo koji posao obavljaju.

Počnimo sa statičkim trenjem. Ovaj tip se manifestuje kada se tijelo ne kreće. Pošto nema kretanja, njegov vektor pomaka l¯ jednak je nuli. Ovo posljednje znači da je rad sile statičkog trenja također jednak nuli.

Trenje klizanja, po definiciji, djeluje samo kada se tijelo kreće u prostoru. Kako je sila ove vrste trenja uvijek usmjerena protiv kretanja tijela, to znači da ono radi negativan rad. Vrijednost A može se izračunati pomoću formule:

A=-F_tl=-µ_tNl.

Rad sile trenja klizanja ima za cilj usporavanje kretanja tijela. Kao rezultat ovog rada, mehanička energija tijela se pretvara u toplinu.

Trenje kotrljanja, poput klizanja, također uključuje kretanje tijela. Sila trenja kotrljanja obavlja negativan rad, usporavajući početnu rotaciju tijela. Pošto je riječ o rotaciji tijela, zgodno je izračunati vrijednost rada ove sile kroz rad njenog momenta. Odgovarajuća formula se piše kao:

A=-Mθ gdje je M=F_tR.

Ovde je θ ugao rotacije tela kao rezultat rotacije, R je rastojanje od površine do ose rotacije (poluprečnik točka).

Problem sa silom trenja klizanja

Poznato je da se drveni blok nalazi na ivici nagnute drvene ravni. Avion je nagnut prema horizontu pod uglom od 40o. Znajući da je koeficijent trenja klizanja 0,4, dužina ravni 1 metar, a masa šipke odgovara 0,5 kg, potrebno je pronaći rad trenja klizanja.

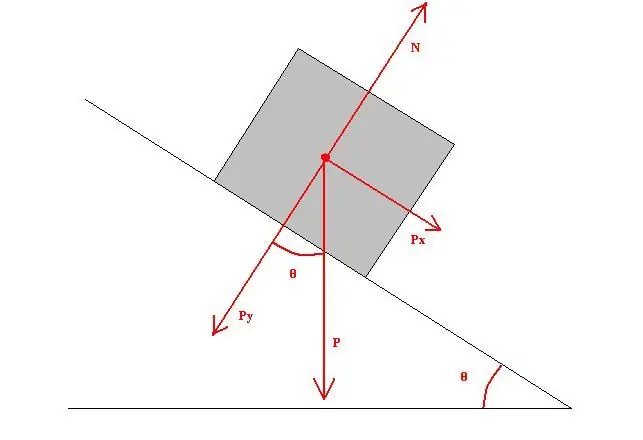
Izračunajte silu trenja klizanja. Jednako je:

F_t=mgcos(α)µ_t=0.59.81cos(40 ^{o)0, 4=1,5 N.}

Tada će odgovarajući rad A biti:

A=-F_{tl=-1,51=-1,5 J.}

Problem sa trenjem kotrljanja

Poznato je da se točak otkotrljao po putu na nekoj udaljenosti i zaustavio se. Prečnik točka je 45 cm Broj obrtaja točka pre zaustavljanja je 100. Uzimajući u obzir koeficijent kotrljanja jednak 0,03, potrebno je pronaći koliko je jednak rad sile trenja kotrljanja. Masa točka je 5 kg.

Prvo, izračunajmo moment trenja kotrljanja:

M=F_tR=µ_{tmgD/2=0,0359, 81 0, 45/2=0, 331 Nm.}

Ako se broj obrtaja koje napravi točak pomnoži sa 2pi radijana, onda dobijamo ugao rotacije točka θ. Tada je formula za rad:

A=-Mθ=-M2pin.

Gdje je n broj okretaja. Zamjenom momenta M i broja n iz uslova dobijamo traženi rad: A=- 207,87 J.