Modul elastičnosti je fizička veličina koja karakterizira elastično ponašanje materijala kada se na njega primjenjuje vanjska sila u određenom smjeru. Elastično ponašanje materijala znači njegovu deformaciju u području elastičnosti.
Istorija proučavanja elastičnosti materijala

Fizičku teoriju elastičnih tijela i njihovo ponašanje pod djelovanjem vanjskih sila detaljno je razmatrao i proučavao engleski naučnik iz 19. stoljeća Thomas Young. Međutim, sam koncept elastičnosti razvio je davne 1727. godine švicarski matematičar, fizičar i filozof Leonhard Euler, a prvi eksperimenti vezani za modul elastičnosti izvedeni su 1782. godine, odnosno 25 godina prije rada Thomasa Junga., venecijanskog matematičara i filozofa Jacopa Ricattija.
Zasluga Thomasa Younga leži u činjenici da je teoriji elastičnosti dao vitak moderan izgled, koji je kasnije formaliziran u obliku jednostavnog, a zatim generaliziranog Hookeovog zakona.
Fizička priroda elastičnosti
Svako tijelo se sastoji od atoma, između kojih djeluju sile privlačenja i odbijanja. Ravnoteža ovih sila jestanje i parametri materije pod datim uslovima. Atomi čvrstog tijela, kada se na njih primjenjuju neznatne vanjske sile zatezanja ili kompresije, počinju se pomicati, stvarajući silu suprotnog smjera i jednake veličine, koja teži da vrati atome u početno stanje.
U procesu takvog pomjeranja atoma povećava se energija cijelog sistema. Eksperimenti pokazuju da je pri malim deformacijama energija proporcionalna kvadratu ovih deformacija. To znači da se sila, kao derivacija u odnosu na energiju, ispostavlja da je proporcionalna prvom stepenu deformacije, odnosno da linearno zavisi od nje. Odgovarajući na pitanje, koliki je modul elastičnosti, možemo reći da je to koeficijent proporcionalnosti između sile koja djeluje na atom i deformacije koju ta sila uzrokuje. Dimenzija Youngovog modula je ista kao i dimenzija pritiska (Pascal).
Elastično ograničenje
Prema definiciji, modul elastičnosti pokazuje koliko naprezanja mora biti primijenjeno na čvrsto tijelo da bi njegova deformacija bila 100%. Međutim, sve čvrste tvari imaju granicu elastičnosti jednaku 1% deformacije. To znači da ako se primijeni odgovarajuća sila i tijelo se deformiše za iznos manji od 1%, onda nakon prestanka ove sile tijelo potpuno vraća svoj prvobitni oblik i dimenzije. Ako se primijeni prevelika sila, pri kojoj vrijednost deformacije prelazi 1%, nakon prestanka vanjske sile, tijelo više neće vratiti svoje prvobitne dimenzije. U potonjem slučaju se govori o postojanju zaostale deformacije, tjdokaz da je granica elastičnosti materijala prekoračena.
Youngov modul u akciji
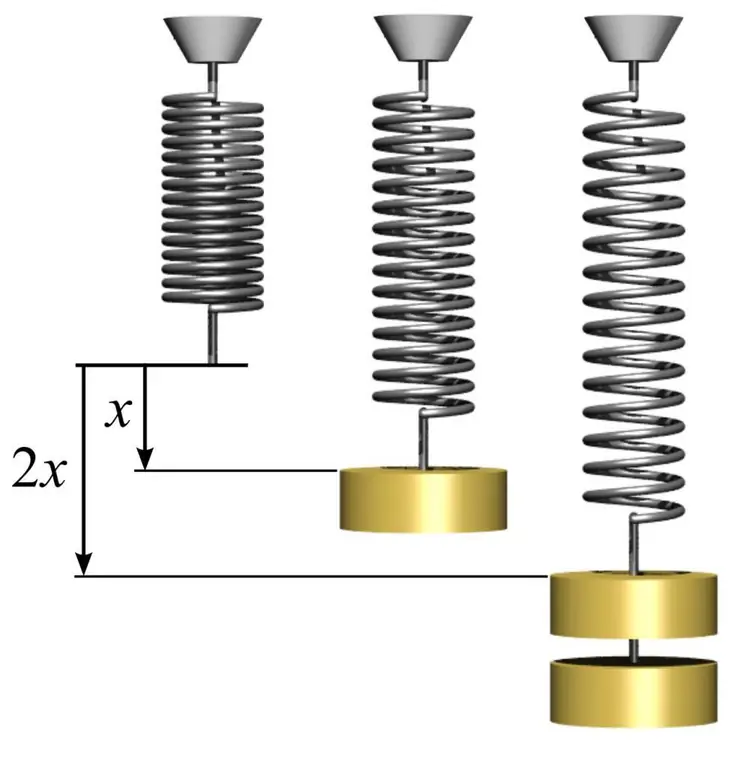
Da biste odredili modul elastičnosti, kao i da biste razumjeli kako ga koristiti, možete dati jednostavan primjer sa oprugom. Da biste to učinili, trebate uzeti metalnu oprugu i izmjeriti površinu kruga koji formiraju njegovi zavojci. Ovo se radi pomoću jednostavne formule S=πr², gdje je n pi jednako 3,14, a r je polumjer namotaja opruge.
Dalje izmjerite dužinu opruge l0 bez opterećenja. Ako okačite bilo koji teret mase m1 na oprugu, tada će ona povećati svoju dužinu na određenu vrijednost l1. Modul elastičnosti E može se izračunati na osnovu poznavanja Hookeovog zakona po formuli: E=m1gl0/(S(l 1-l0)), gdje je g ubrzanje slobodnog pada. U ovom slučaju, napominjemo da količina deformacije opruge u elastičnom području može uveliko premašiti 1%.
Poznavanje Youngovog modula omogućava vam da predvidite količinu deformacije pod dejstvom određenog naprezanja. U ovom slučaju, ako okačimo drugu masu m2 na oprugu, dobijamo sljedeću vrijednost relativne deformacije: d=m2g/ (SE), gdje je d - relativna deformacija u elastičnom području.
Izotropija i anizotropija
Modul elastičnosti je karakteristika materijala koja opisuje snagu veze između njegovih atoma i molekula, međutim određeni materijal može imati nekoliko različitih Youngovih modula.
Činjenica je da svojstva svake čvrste supstance zavise od njene unutrašnje strukture. Ako su svojstva ista u svim prostornim pravcima, onda govorimo o izotropnom materijalu. Takve tvari imaju homogenu strukturu, pa djelovanje vanjske sile u različitim smjerovima na njih izaziva istu reakciju materijala. Svi amorfni materijali su izotropni, kao što je guma ili staklo.
Anizotropija je pojava koju karakteriše zavisnost fizičkih svojstava čvrste ili tečnosti o pravcu. Svi metali i legure na njihovoj osnovi imaju jednu ili drugu kristalnu rešetku, odnosno uređen, a ne kaotičan raspored ionskih jezgara. Kod takvih materijala modul elastičnosti varira ovisno o osi djelovanja vanjskog naprezanja. Na primjer, metali sa kubičnom simetrijom, kao što su aluminijum, bakar, srebro, vatrostalni metali i drugi, imaju tri različita Youngova modula.
modul smicanja
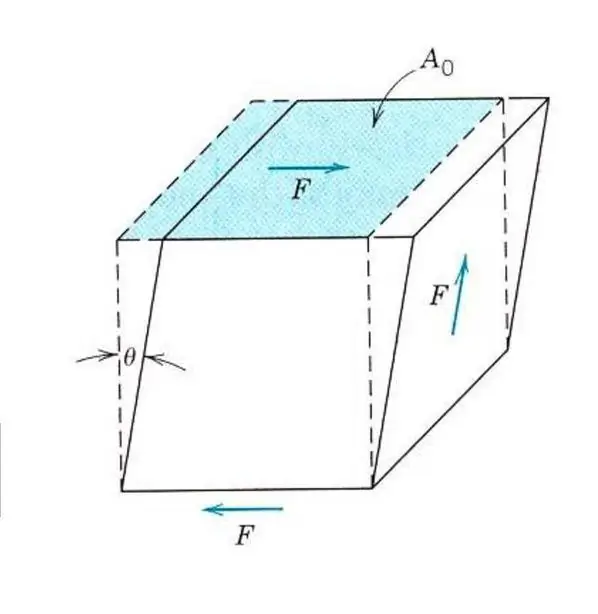
Opis elastičnih svojstava čak i izotropnog materijala ne zahtijeva poznavanje jednog Youngovog modula. Jer, osim zatezanja i kompresije, na materijal mogu utjecati naprezanja smicanja ili torzijska naprezanja. U ovom slučaju će drugačije reagirati na vanjsku silu. Da bi se opisala elastična posmična deformacija, uvodi se analog Youngovog modula, modula smicanja ili modula elastičnosti druge vrste.
Svi materijali su otporni na posmična naprezanja manja od napetosti ili kompresije, tako da je vrijednost modula smicanja za njih 2-3 puta manja od vrijednosti Youngovog modula. Dakle, za titan, čiji je Youngov modul jednak 107 GPa, modul smicanja jesamo 40 GPa, za čelik ove brojke su 210 GPa i 80 GPa, respektivno.
Modul elastičnosti drveta

Drvo je anizotropan materijal jer su drvena vlakna orijentirana duž određenog smjera. Uzduž vlakana se mjeri modul elastičnosti drveta, jer je po vlaknima manji za 1-2 reda veličine. Poznavanje Youngovog modula za drvo je važno i uzima se u obzir prilikom projektovanja drvenih panelnih struktura.
Vrijednosti modula elastičnosti drveta za neke vrste drveća prikazane su u tabeli ispod.
| Pregled drveta | Youngov modul u GPa |
| Lovorovo drvo | 14 |
| Eukaliptus | 18 |
| Cedar | 8 |
| Smreka | 11 |
| Pine | 10 |
| Hrast | 12 |
Treba imati na umu da se date vrijednosti mogu razlikovati do 1 GPa za određeno drvo, budući da na njegov Youngov modul utiče gustina drveta i uslovi rasta.

Moduli smicanja za razne vrste drveća su u rasponu od 1-2 GPa, na primjer, za bor je 1,21 GPa, a za hrast 1,38 GPa, odnosno drvo praktički ne odolijeva posmičnim naprezanjima. Ova činjenica se mora uzeti u obzir pri proizvodnji drvenih nosivih konstrukcija, koje su dizajnirane da rade samo na napetost ili kompresiju.
Elastične karakteristike metala
U poređenju sa Youngovim modulom drveta, prosječne vrijednosti ove vrijednosti za metale i legure su za red veličine veće, kao što je prikazano u sljedećoj tabeli.
| Metal | Youngov modul u GPa |
| Bronza | 120 |
| Bakar | 110 |
| Čelik | 210 |
| Titanium | 107 |
| Nikal | 204 |
Elastična svojstva metala koji imaju kubičnu singoniju opisuju se sa tri elastične konstante. Takvi metali uključuju bakar, nikal, aluminijum, gvožđe. Ako metal ima heksagonalnu singoniju, tada je već potrebno šest konstanti da opiše njegove elastične karakteristike.
Za metalne sisteme, Youngov modul se mjeri unutar 0,2% deformacije, pošto se velike vrijednosti već mogu pojaviti u neelastičnom području.






