Idealni gas, jednačina stanja idealnog gasa, njegova temperatura i pritisak, zapremina… lista parametara i definicija korišćenih u odgovarajućem delu fizike može se nastaviti još dugo. Danas ćemo pričati samo o ovoj temi.
Šta se smatra u molekularnoj fizici?

Glavni objekat razmatran u ovom odeljku je idealan gas. Jednačina stanja idealnog gasa dobijena je uzimajući u obzir normalne uslove okoline, a o tome ćemo nešto kasnije. Sada pristupimo ovom "problemu" izdaleka.
Recimo da imamo neku masu gasa. Njegovo stanje se može odrediti korištenjem tri parametra termodinamičke prirode. To su, naravno, pritisak, zapremina i temperatura. Jednačina stanja sistema u ovom slučaju će biti formula za odnos između odgovarajućih parametara. To izgleda ovako: F (p, V, T)=0.
Evo, po prvi put, polako se približavamo nastanku nečeg kao idealnoggas. Naziva se plinom u kojem su interakcije između molekula zanemarljive. Općenito, to ne postoji u prirodi. Međutim, svaki visoko razrijeđeni plin mu je blizu. Azot, kiseonik i vazduh, koji su u normalnim uslovima, malo se razlikuju od idealnih. Da bismo napisali jednačinu stanja idealnog gasa, možemo koristiti jedinstveni zakon o gasu. Dobijamo: pV/T=konst.
Povezan koncept 1: Avogadrov zakon
On nam može reći da ako uzmemo isti broj molova apsolutno bilo kojeg slučajnog plina i stavimo ih u iste uslove, uključujući temperaturu i pritisak, tada će plinovi zauzeti istu zapreminu. Konkretno, eksperiment je izveden u normalnim uslovima. To znači da je temperatura bila 273,15 Kelvina, pritisak je bio jedna atmosfera (760 milimetara žive ili 101325 Paskala). Sa ovim parametrima, gas je zauzimao zapreminu jednaku 22,4 litara. Stoga možemo reći da će za jedan mol bilo kojeg plina omjer numeričkih parametara biti konstantna vrijednost. Zato je odlučeno da se ova brojka označi slovom R i nazove je univerzalna plinska konstanta. Dakle, to je jednako 8,31 Jedinica je J/molK.
Idealan gas. Idealna plinska jednadžba stanja i njena manipulacija
Pokušajmo da prepišemo formulu. Da bismo to učinili, pišemo ga u ovom obliku: pV=RT. Zatim izvodimo jednostavnu radnju, množimo obje strane jednadžbe sa proizvoljnim brojem molova. Dobijamo pVu=uRT. Uzmimo u obzir činjenicu da je proizvod molarne zapremine ikoličina materije je jednostavno volumen. Ali na kraju krajeva, broj molova će istovremeno biti jednak količniku mase i molarne mase. Upravo ovako izgleda Mendeljejev-Klapejronova jednačina. Daje jasnu predstavu o tome kakav sistem formira idealan gas. Jednačina stanja za idealni gas će imati oblik: pV=mRT/M.
Izvedite formulu za pritisak
Napravimo još neke manipulacije sa dobijenim izrazima. Da biste to učinili, desna strana Mendelejev-Clapeyronove jednadžbe se množi i dijeli s Avogadrovim brojem. Sada pažljivo gledamo proizvod količine tvari prema Avogadrovom broju. Ovo nije ništa drugo do ukupan broj molekula u gasu. Ali u isto vrijeme, omjer univerzalne plinske konstante i Avogadrovog broja bit će jednak Boltzmannovoj konstanti. Stoga se formule za pritisak mogu napisati na sljedeći način: p=NkT/V ili p=nkT. Ovdje je simbol n koncentracija čestica.
Idealni gasni procesi
U molekularnoj fizici postoji takva stvar kao što su izoprocesi. To su termodinamički procesi koji se odvijaju u sistemu pri jednom od konstantnih parametara. U tom slučaju, masa tvari također mora ostati konstantna. Pogledajmo ih konkretnije. Dakle, zakoni idealnog gasa.
Pritisak ostaje konstantan
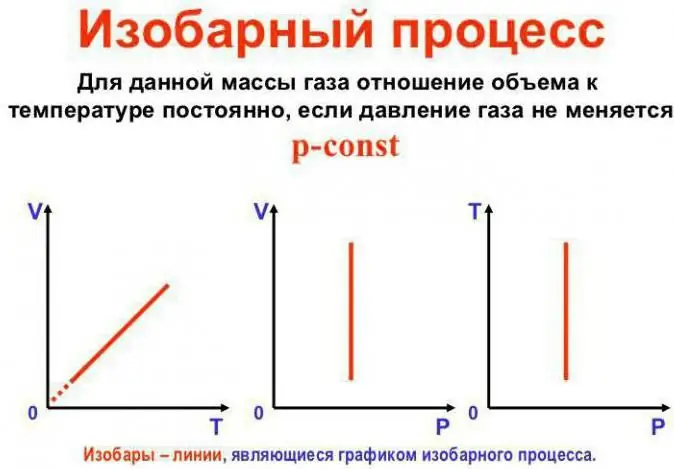
Ovo je Gay-Lussacov zakon. To izgleda ovako: V/T=konst. Može se prepisati i na drugi način: V=Vo (1 + at). Ovdje je a jednako 1/273,15 K^-1 i naziva se "koeficijent proširenja zapremine". Temperaturu možemo zamijeniti i u Celzijusima i uKelvinovu skalu. U potonjem slučaju dobijamo formulu V=Voat.
Obim ostaje konstantan

Ovo je drugi Gay-Lussacov zakon, koji se češće naziva Charlesov zakon. To izgleda ovako: p/T=const. Postoji još jedna formulacija: p=po (1 + at). Transformacije se mogu izvesti u skladu s prethodnim primjerom. Kao što vidite, zakoni o idealnom plinu su ponekad prilično slični jedni drugima.
Temperatura ostaje konstantna

Ako temperatura idealnog gasa ostane konstantna, tada možemo dobiti Boyle-Mariotteov zakon. Može se napisati ovako: pV=const.
Povezan koncept 2: Parcijalni pritisak
Recimo da imamo posudu sa gasovima. To će biti mješavina. Sistem je u stanju termičke ravnoteže, a sami gasovi ne reaguju jedni na druge. Ovdje će N označavati ukupan broj molekula. N1, N2 i tako dalje, redom, broj molekula u svakoj od komponenti smjese. Uzmimo formulu pritiska p=nkT=NkT/V. Može se otvoriti za konkretan slučaj. Za dvokomponentnu smjesu, formula će imati oblik: p=(N1 + N2) kT/V. Ali onda se ispostavi da će se ukupni pritisak zbrojiti iz parcijalnih pritisaka svake mješavine. Dakle, izgledat će kao p1 + p2 i tako dalje. Ovo će biti parcijalni pritisci.
Za šta služi?
Formula koju smo dobili pokazuje da je pritisak u sistemu iz svake grupe molekula. Uzgred, ne zavisi oddrugi. D alton je to iskoristio kada je formulisao zakon, kasnije nazvan po njemu: u smjesi u kojoj plinovi ne reagiraju kemijski jedni s drugima, ukupan pritisak će biti jednak zbiru parcijalnih pritisaka.






