Kada proučavaju fiziku mehaničko kretanje tijela u prostoru, uvijek uzimaju u obzir rezultirajuće ubrzanje. Razmotrimo u članku šta je ubrzanje i kako se označava u fizici, a također riješimo jednostavan problem za izračunavanje ove vrijednosti.
Šta je ubrzanje i koje su njegove vrste?
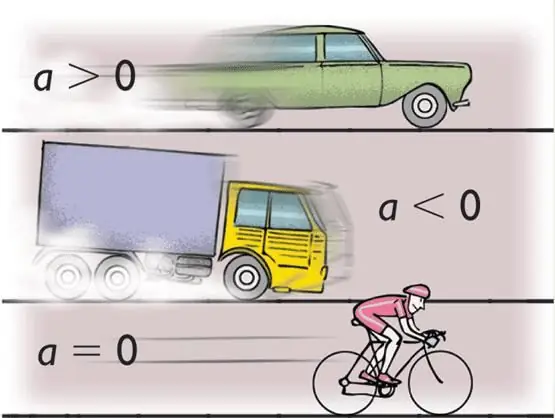
Pod ubrzanjem podrazumijeva se vrijednost, čije je značenje brzina promjene brzine tijela. Matematički, ova definicija je napisana na sljedeći način:
a=dv/dt.
Ako je poznata vremenska funkcija brzine, dovoljno je pronaći njen prvi izvod da bi se izračunalo ubrzanje u datom trenutku.
U fizici, slovo ubrzanja je malo latinično a. Međutim, ovo je takozvano linearno ubrzanje, koje se mjeri u jedinicama m/s2. Osim toga, postoji i ugaona ubrzanja. Pokazuje promjenu ugaone brzine i izražava se u jedinicama rad/s2. Ova vrsta ubrzanja je označena grčkim malim slovom α (alfa). Ponekadslovo ε (epsilon) se koristi da ga označi.
Ako se tijelo kreće duž zakrivljene putanje, tada se ukupno ubrzanje razlaže na dvije komponente: tangencijalnu (određuje promjenu brzine u veličini) i normalnu (određuje promjenu brzine u smjeru). Ove vrste ubrzanja su takođe označene slovima a, ali koristeći odgovarajuće indekse: at i a. Normalna se često naziva centripetalna, a tangencijalna se često naziva tangentna.
Konačno, postoji još jedna vrsta ubrzanja koja se javlja kada tijela slobodno padaju u gravitacionom polju planete. Označava se slovom g.
Problem u fizici za ubrzanje
Poznato je da se tijelo kreće pravolinijski. Njegova brzina tokom vremena određena je sljedećim zakonom:
v=2t2-t+4.
Potrebno je izračunati ubrzanje koje će tijelo imati u vremenu t=2,5 sekunde.
Slijedeći definiciju a, dobijamo:
a=dv/dt=4t - 1.
To jest, vrijednost a zavisi linearno od vremena. Zanimljivo je primijetiti da je u početnom trenutku (t=0) ubrzanje bilo negativno, odnosno usmjereno prema vektoru brzine. Dobijamo odgovor na problem zamjenom t=2,5 sekunde u ovu jednačinu: a=9 m/s2.






